선택정렬(Selection Sort)

Selection Sort

정렬할 위치를 먼저 선택한 뒤 그 자리에 오는 값을 찾고(Compare) 값이 있다면 교환(Swap)하는 방식의 알고리즘입니다.

 

Process

1부터 6까지 랜덤으로 들어 있는 배열이 있습니다.

Ascending(오름차순)으로 정렬합니다.

 

 

오름차순 이기 때문에 0번 인덱스부터 최소값으로 정렬 되어야 합니다.

1. 0번 인덱스에 넣을 최소 값의 인덱스를 찾습니다.
2. 0번 인덱스의 아이템이 최소 값이 아니라면 최소값이 위치한 인덱스의 값과 교환합니다. - 가장 작다면 교환 하지 않습니다.

여기까지 1 사이클입니다.

 

이제 0번 인덱스는 정렬이 완료되었기 때문에 1번 인덱스부터 최소 값을 찾습니다.

최소 값이 다른 인덱스라면 값을 Swap 합니다.

 

정렬이 완료될 때까지 위의 사이클을 반복합니다.

 

Code

void selectionSort(int arr[], int length)
{
    int minIndex = 0;
    int temp = 0;
    
    for (int i=0; i < length; i++) // 정렬하고자 하는 위치를 선택한다.
    {
        minIndex = i;
        
        for (int j= i + 1; j < length; j++) // 정렬하고자 하는 위치 다음부터 값을 비교한다
        {
            if (arr[minIndex] > arr[j]) // 오른차순이므로 최소값을 찾으면 인덱스를 갱신한다.
            {
                minIndex = j;
            }
        }
        
        if (i != minIndex) // 최소값이 다른 위치에 있으면 swap
        {
            temp = arr[minIndex];
            arr[minIndex] = arr[i];
            arr[i] = temp;
        }
    }
}

 

Time Complexity of Selection Sort

Selection Sort는 반복문이 두 번 있는 케이스이고, 배열의 정렬 여부와 관계없이 모든 값을 비교해야 하므로 O(n^2)입니다.

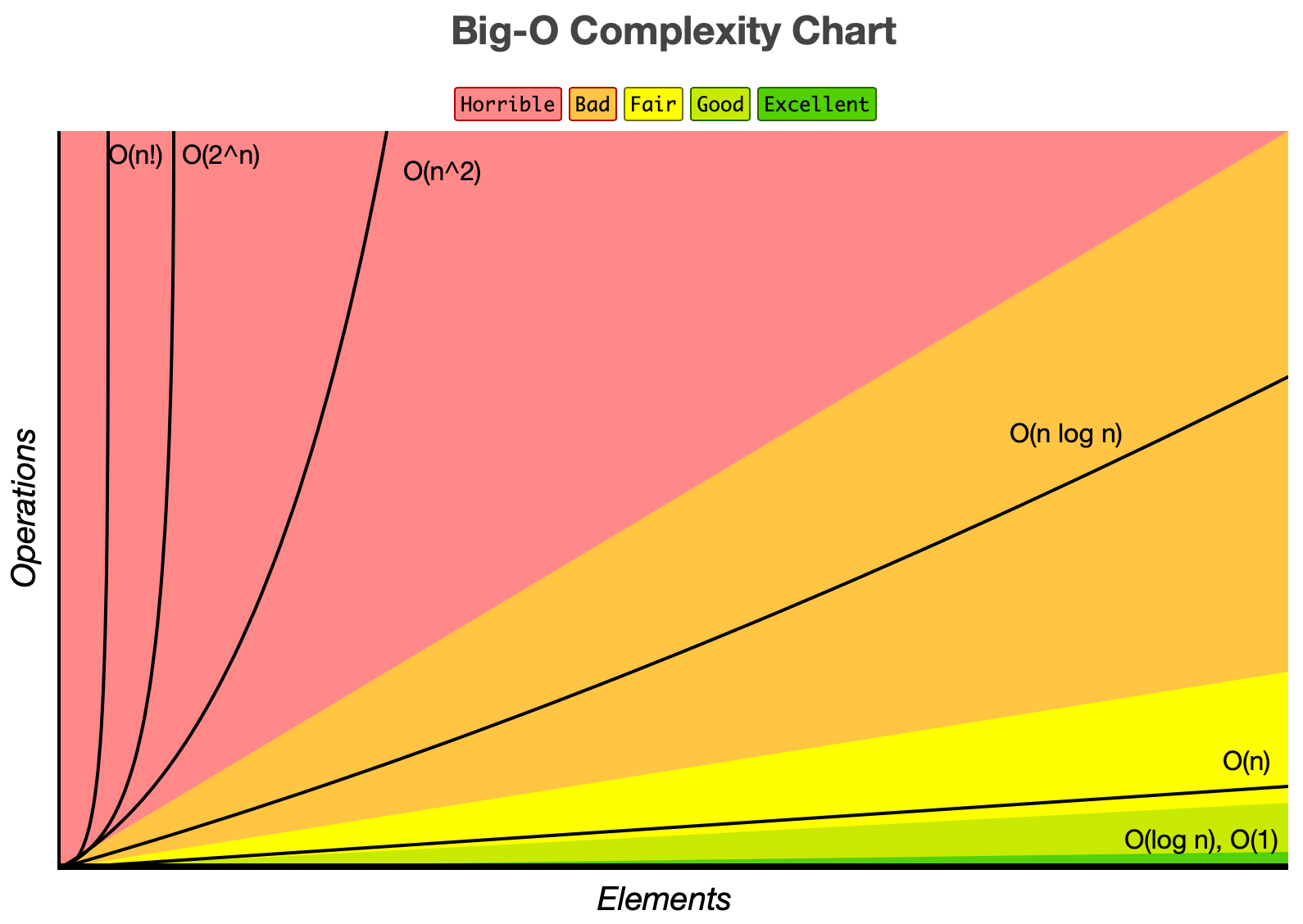
https://www.bigocheatsheet.com

참고

• https://blog.chulgil.me/algorithm/
• https://www.bigocheatsheet.com